Operating Systems. Exercises.

I. C言語復習(準備課題, 配点無し)
演習問題を解くために必要な、基本的なC言語の文法をいくつか復習をする課題です。
配点はありません。ここで扱うことがわかっていれば飛ばして、II(下方)のハノイの塔だけ解いてください。

例題1
コマンドライン引数の取り方を確認します。コマンドライン引数を取って表示するプログラムを書いてください。 (テンプレート)

例: プログラムの実行形式のファイル名を "ArgPrint"とし, 引数を"1", "2", "3"としたとき

コマンド


	% ./ArgPrint 1 2 3

結果


	引数の数 : 4
	引数0 = ./ArgPrint
	引数1 = 1
	引数2 = 2
	引数3 = 3

例題2
配列の動的確保の仕方を確認します。整数ポインタにコマンドライン引数個要素の整数配列を動的に割り当て,
配列の中身を2の配列添字乗にしてから出力してください。 (テンプレート)

例: プログラムの実行形式のファイル名を "ArrayAlloc"とし, 引数を"8"としたとき

コマンド


	% ./ArrayAlloc 8

結果


	2の0乗 : 1
	2の1乗 : 2
	2の2乗 : 4
	2の3乗 : 8
	2の4乗 : 16
	2の5乗 : 32
	2の6乗 : 64
	2の7乗 : 128
	2の8乗 : 256

II. ハノイの塔(配点100%)

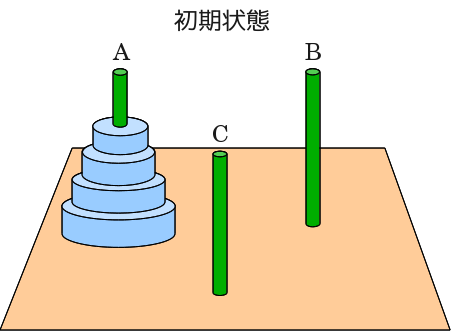
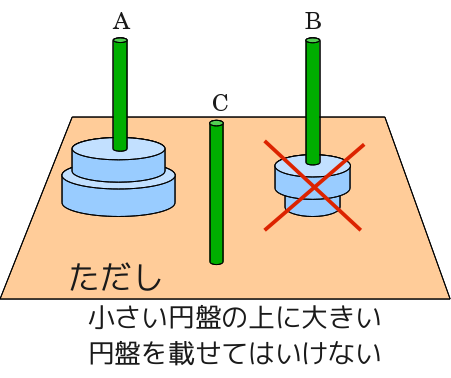
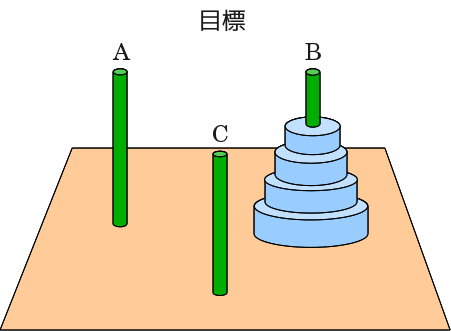
ハノイの塔は小さい円盤の上に大きい円盤載せないようにしながら円盤を一つずつ移動し、
穴の開いたn個の円盤を棒Aから棒Bに遷すもので、補助として棒Cを使う

課題
テンプレートプログラムは円盤数を5に固定した整数配列を使ってハノイの塔の問題を解くプログラムである。

これをコマンドライン引数で円盤数nを与え、その分の整数配列を動的に確保し円盤数nのハノイの塔の問題を解けるように改変してください。

例 : 円盤数"nDisks"は, コマンドライン引数として与えられるようにします.
棒A, B, CをnDisks個要素の整数配列で表現します.
配列nDisks-1番目には一番小さい円盤, 配列0番目には一番大きい円盤が入っています.
円盤を数字1からnDisksで表しています. 円盤が無い場所には0が入っています.

以下がプログラムの実行形式のファイル名を "hanoi"として、円盤が8個の場合のコマンドと出力です

コマンド


      % ./hanoi 8

結果


      初期状態
      | 1|   | 0|   | 0| 
      | 2|   | 0|   | 0| 
      | 3|   | 0|   | 0| 
      | 4|   | 0|   | 0| 
      | 5|   | 0|   | 0| 
      | 6|   | 0|   | 0| 
      | 7|   | 0|   | 0| 
      | 8|   | 0|   | 0| 
      ----   ----   ---- 
      A      B      C 
      Number of Moves: 0
      Numer of Disks: 8

(こういう状態を表している)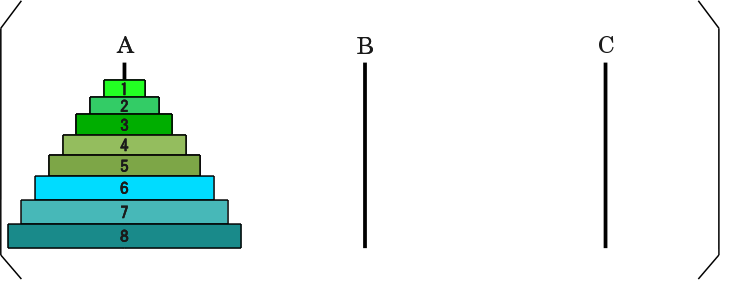


      完成
      | 0|   | 1|   | 0|
      | 0|   | 2|   | 0|
      | 0|   | 3|   | 0|
      | 0|   | 4|   | 0|
      | 0|   | 5|   | 0|
      | 0|   | 6|   | 0|
      | 0|   | 7|   | 0|
      | 0|   | 8|   | 0|
      ----   ----   ----
      A      B      C
      Number of Moves: 255
      Numer of Disks: 8

(こういう状態を表している)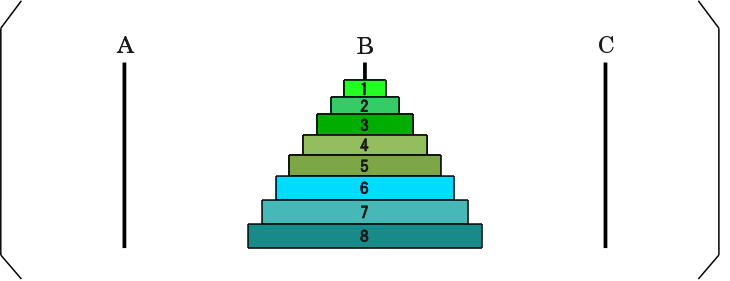

ハノイの塔の解法について

[自分でも紙に書いて処理をを追ってみると良いでしょう。]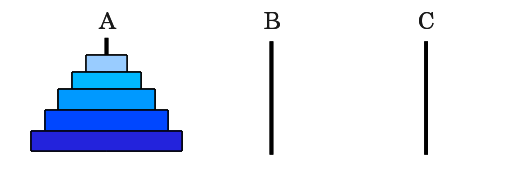

図には円盤が5つしかありませんが, n個あると思ってください. 初期状態で円盤は全てAにあって, Bが目標移動地点で, Cが補助とします

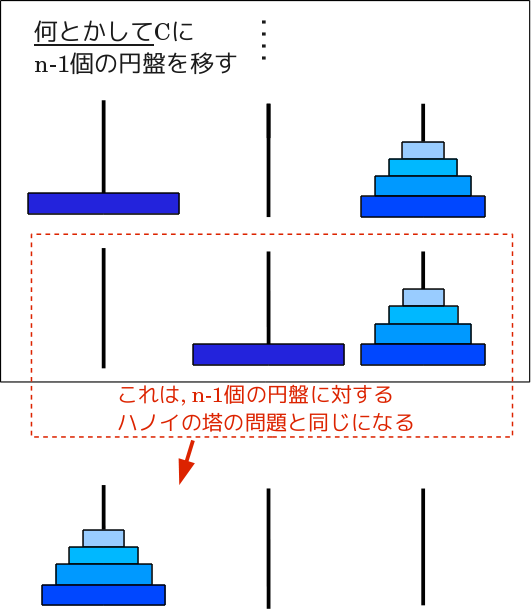A, B, Cを利用して何とかしてn-1個の円盤をAからCに移すと, n番目の円盤をBに移すことが出来ます. n番目の円盤は一番大きく, その上には他のどの円盤でも置けるので, これは初期地点Aと補助Cの場所が入れ替わった, n-1個の円盤のときのハノイの塔の問題になります.

今度は何とかしてn-2個の円盤をCからAに移してやればn-1番目の円盤を Bに置くことができる, というふうに再帰的に解くことが出来ます.