Sound Localization in Reverberant Environments

• Background Sound localization is an important function of the auditory system of a mobile robot and can also be used for a teleconference system to guide its camera to pick up the faces of speakers automatically. In such practical applications, sound localization is usually performed in reverberant environments. The major approach for sound source localization is through time correlation between different receiving channels. However, traditional cross correlation methods are less effective in low sound-noise ratio environments and being affected by echoes and reverberations. Those methods can not localize multiple sources concurrently.

  
  

• How to cope with echoes? When a sound is presented in a reverberant environment, human listeners usually can localize the sound at the correct source position, little influenced by the surrounding reflections. This phenomenon is referred to as the "precedence effect". The precedence effect can give important suggestions for computational sound localization in a reverberant environment. Here we describe a simple echo estimation method adopted from the echo-avoidance computational model of the precedence effect.

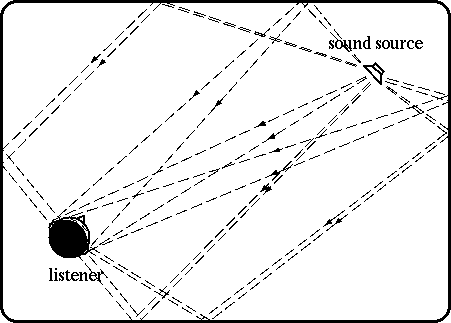
  When the impulse response from the sound source to the ear is defined as h(t), and the part caused by echoes (removed the effect of the direct sound from the the impulse response) is h_e(t). The echoes of a sound signal s(t) is given as
  s_e(t) = h_e(t) * s(t).
  Although the impulse response here is unknow, we can give an generalized approximation which reflects the delay and decay features in the impulse response
  g_e = k e ^-(t-t0)/tau.
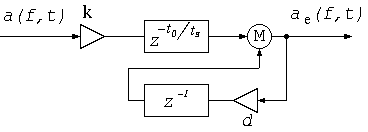
  Here, the delay time t₀ and decay factor tau are chosen to match the most general cases in an ordinary environment. (It is done by the learning effect in the human auditory systems.) Thus, the echoes of a subband signal a(f,t) (envelop of narrow-subband signal or amplitude of short-term Fourier transform) can be estimated as
  a_e(f,t) = Max{a(f,t-t') g_e(t')} for 0 < t' < inf.
  By using the exponential decay feature of the generalized impulse response, the echo estimation algorithm can be implemented by a feed-back manner, where t_s is the sampling time interval and d = e ^-ts/tou.

  
  

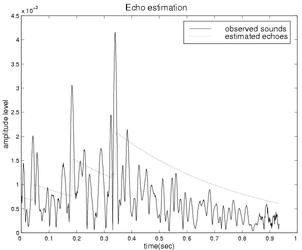
  The following figure shows an example of echo estimation.

  
  

• Sound localization method

  
  

• Sound localization experiments

  
  

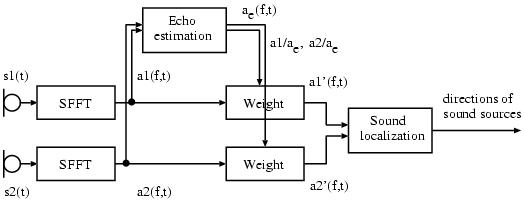
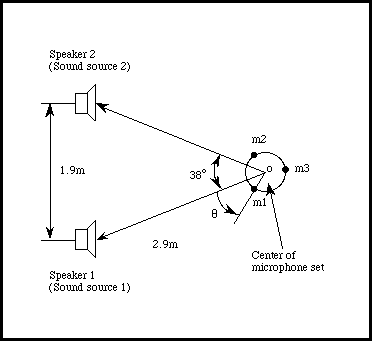
  • Sound Source 1: Radio weather forecast
  • Sound Source 2: Talk show with one male and one female host

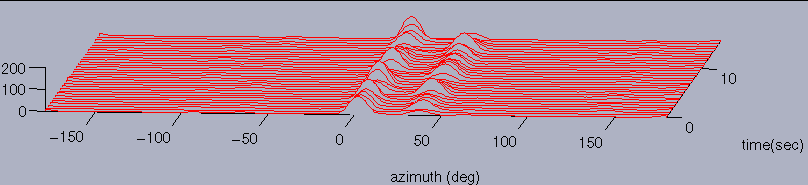
  Localization results in an anechoic chamber

  
  

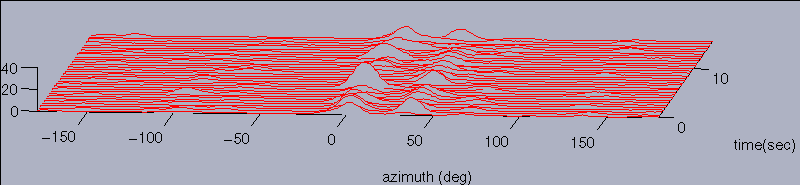
  Localization results in a normal room

  
  

• Reference:
  
  • Huang, J. and Supaongprapa, T. and Terakura, I and Wang, F. and Ohnishi, N. and Sugie, N., "A Model Based Sound Localization System and Its Application to Robot Navigation", Robotics and Autonomous Systems (Elsevier Science), Vol.27, No.4, pp.199-209, 1999.

  • Jie Huang, Noboru Ohnishi and Noboru Sugie, "Sound Localization in Reverberant Environment based on the Model of the Precedence Effect", IEEE Trans. Instrumentation and Measurement, Vol.46, No.4, pp.842-846, August 1997.