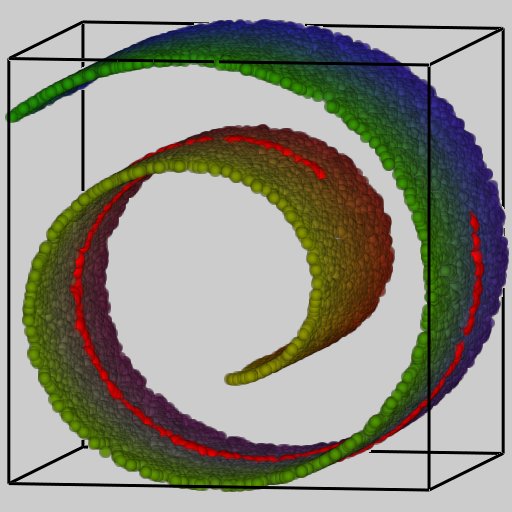
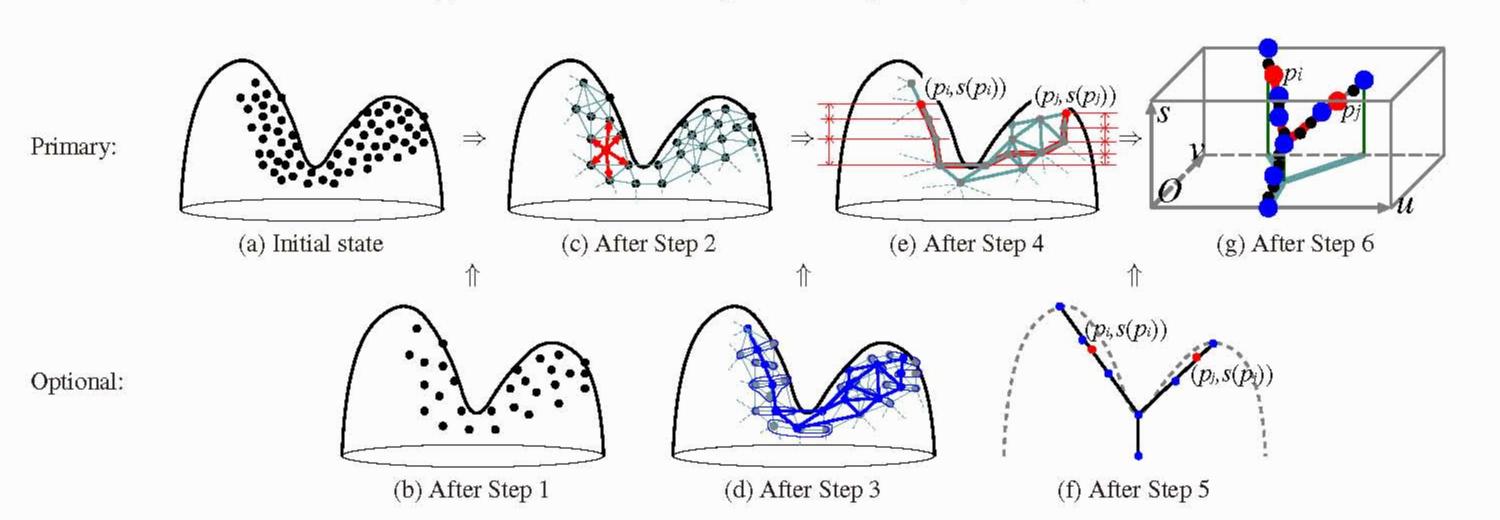
近似 contour tree 構築への多様体学習の応用研究内容画像や地形形状などの2次元のスカラ場, さらにはCTなどの医療用計測機器やシミュレーションで得られるボリュームデータに対応する3次元スカラ場の振る舞いを理解する道具として, coutour tree 呼ばれる位相骨格木が, 形状表現やサイエンティフィックビジュアリゼーションの分野で頻繁に用いられるようになってきました. 従来 contour tree は, 2次元や3次元スカラ場のサンプル点に, 三角形分割あるいは四面体分割などの単体分割を施して線形補間を施して, そののちサンプル点の接続関係を対応するスカラ値の大きさの順に調べていくことで構築されていました. ところが,この contour tree 構築アルゴリズムは, 対象データが時系列変化を伴っていたり, 多くの変数で表現されたりして高次元のデータになった場合には, そのソフトウェアの実装が非常に困難になってしまうという問題がありました.本研究は,この問題を近年注目を集めている非線形次元圧縮手法を適用することで, 解決を図る手法を提案しています. 具体的には,多様体学習とよばれる非線形次元圧縮手法において,サンプル点間の距離の定義を変更することで, 高次元データからの contour tree 構築を実現します. 従来の多様体学習は, 図1(a)のように湾曲している分布をなすサンプル点集合があった場合に, 赤い線で示されているように各サンプル点対間の距離を, サンプル点集合がなす形状(多様体)に沿うパス(測地線)にそって計算することで, 湾曲した分布をまっすぐに延ばした点の分布を, 図1(b)のように低次元空間に変換しています.
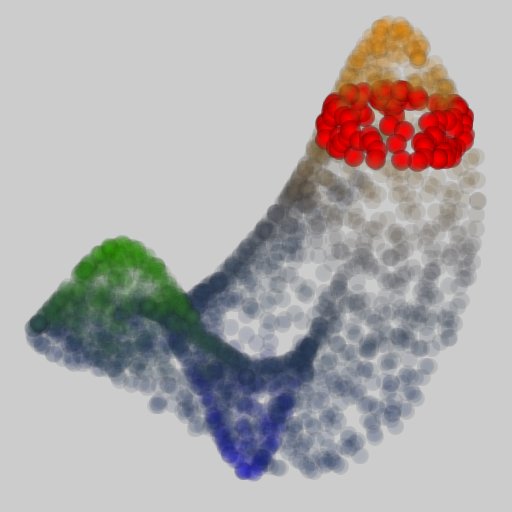
これに対して, contour tree においては, 異なる位置にあるサンプル点も, 同じ等高線あるいは等値面の連結成分内に含まれていれば同一視されるために, 通常のユークリッド距離に基づく距離の定義では計算することができません. 提案手法では, この距離の定義を, サンプル点間の距離が構築されるであろう contour tree 上における距離となるように変更し(図2(e)参照), 新たに contour tree 構築アルゴリズムを定式化したところに新規性が存在します. 例えば,提案手法を用いれば, 図1(c)のような2つの極大値が存在するデータの分布を, 図1(d)のように対応する contour tree (この場合は等高線の高さに関する分岐・併合を表すグラフ) に変換することが可能となります. このように,本手法を用いることで, まったく別個のアルゴリズムを用いて構築されていた contour tree が, 近似表現ではありますが広くデータ解析に一般的に用いられている次元圧縮手法を応用して手軽に構築できるようなりました.
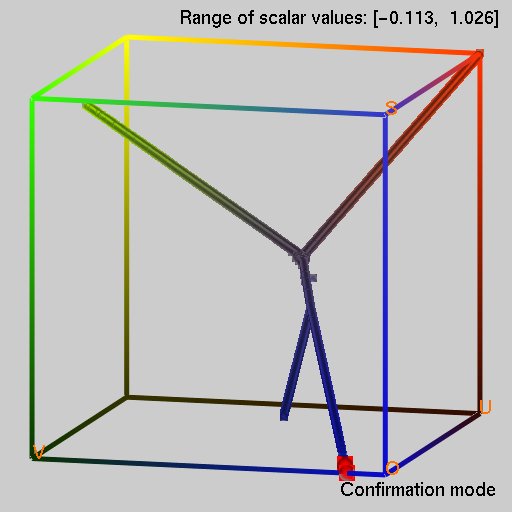
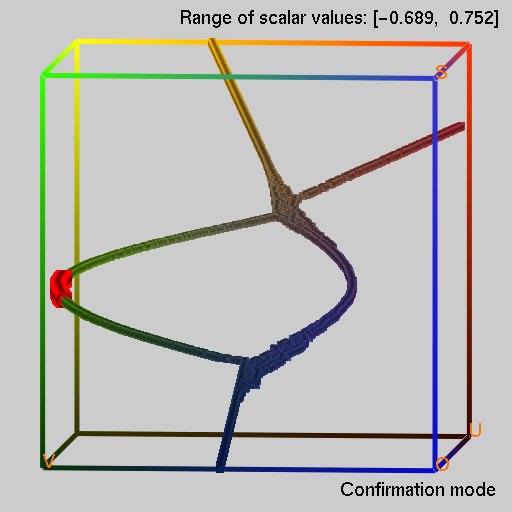
図3は,本手法を適用した事例を示しています. 図3(a)は,ある7次元の関数のサンプル点の集合を3次元空間に写像したものを示しており, 図3(b)は,対応する近似 contour tree を示しています. この関数は,2つの極大値と,2つの極小値を持っているのですが, それが的確に近似 contour tree としてとらえられていることが分かります. 図3(c)は,トーラスのような穴のあいた形状のサンプル点集合を示しています. この場合,対応する位相骨格木は, contour tree から Reeb graph と呼ばれるもっと一般的なグラフ構造となりますが, 図3(d)に示されるように的確に穴の部分をとらえており, 本手法がこのようなトーラス穴を含む形状にも有効であることを示しています.
参考文献
|
|||||||||||||||||||||||||||||||