[Home]->[Project]->[Overlap-free network labeling diagrams]

[English]

ボロノイ分割に基づく重なりのないネットワークのラベル付け

Journal of Visual Languages & Computing, Vol. 44, 2018

このウェブページは， ボロノイ分割に基づく重なりのないネットワークのラベル付け に関するプロジェクトの情報を提供するために準備されたものです


ノードへの注釈ラベルの重なりの除去

ネットワークは，社会的友好関係，研究の共著者関係，合わせて購入する商品の関係など， 抽象的なデータの背後に隠された意味のある特徴をうまくとらえることができます． したがって， そのようなネットワークの視覚化は， 根底にある抽象的な関係を読みやすくする有望な手法と考えられます． 力学指向の手法は， そのような手法の代表的のひとつです． この手法では， ネットワークのノードとエッジに反発力と引力を加えてから， 最終的な平衡状態としてネットワークの配置を見つけ出します． しかしながら， このネットワークのノードにテキストラベルで注釈付けしようとすると， 各ノードの周囲にラベルをつける空間が不足しているために， 注釈ラベルの重なりから生じる視覚的な乱雑さを避けることができません．

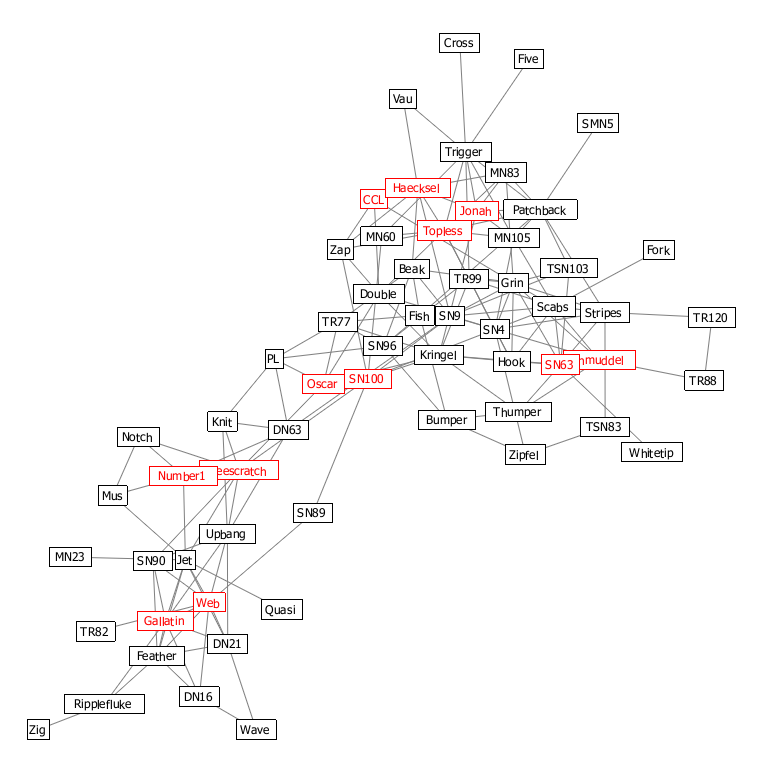
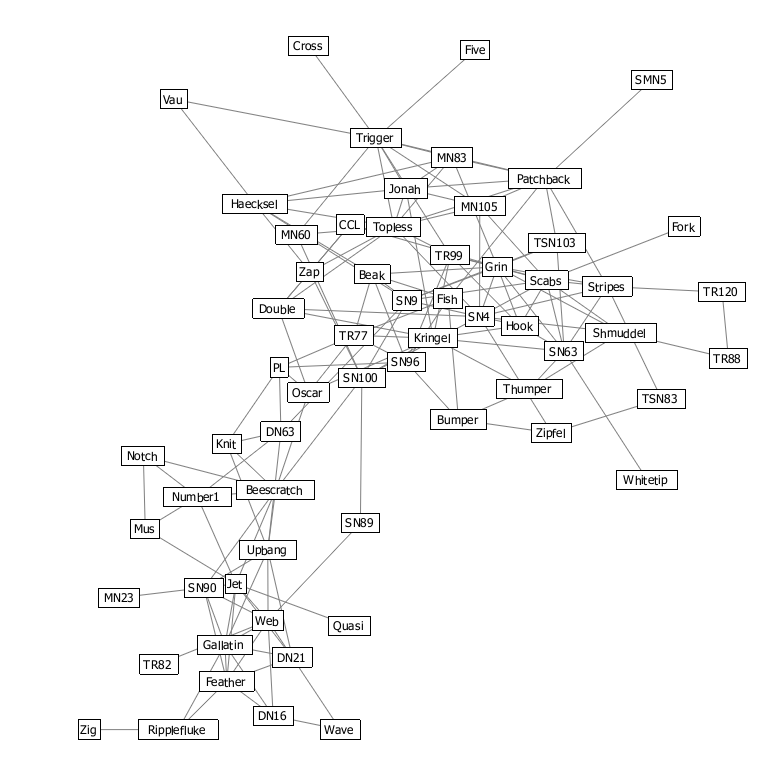
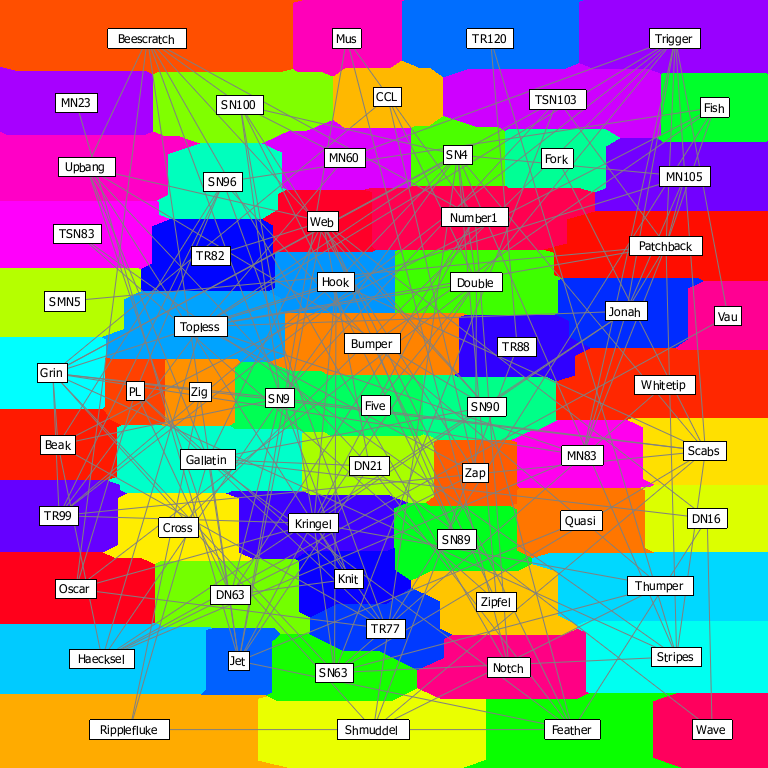
本研究では， ネットワークノードの周囲に十分なラベルを置く空間をを確保することにより， 重なりのないネットワークラベリングへの手法を導入しました． これは， 従来の力学指向の手法と重心ボロノイ分割によって得られたふたつのレイアウト間の， 適切な妥協点を模索することによって達成されます． ネットワークノードに関連付けられたテキストラベルの長方形を最大限尊重するために， 異方性チェビシェフ距離を用いてボロノイ分割を作成します．

図1は， 力学指向レイアウト(図1(a))とボロノイ分割に基づく空間分割(図1(c))の間の合理的な妥協点を求めることにより， 提案手法が注釈付きネットワークの視覚的に適切なレイアウト(図1(b))を生成できる例を示しています． この図に示される通り， 本手法では，元の力学指向レイアウトに比較的近い， コンパクトなネットワークのレイアウトを創出します． さらに， 従来の力学指向レイアウトから誘導された美的基準を最大限に活かしながら， ボロノイ分割に基づく空間分割手法からしばしば生じる， 不等長のエッジや隣接するエッジ間の小さな角度など(図1(c))の望ましくない不自然さを抑制します．

(a) (b) (c)
図1： イルカ間の社会的関係のネットワークレイアウト． (a)力学指向レイアウト． (b)提案手法により生成されたレイアウト． (c)重心ボロノイ分割に基づくレイアウト． 他と重複する注釈ラベルは赤で描画されています．


距離定義の高度化

注釈ラベルのより良い配置を実現するために， ボロノイ分割を生成するための距離定義の選択にいくつかの高度化を行いました． まず，長方形であるノードラベルを配置するときに最も適切な距離定義を選択するために， ユークリッド距離， マンハッタン距離， およびチェビシェフ距離を調べました． ここで，いまふたつのノード ni = xi , yi と nj = xj , yj の距離を考えることにします．このとき， いまの3つの距離の定義は以下のようになります:

dE ni , nj = xi - xj 2 + yi - yj 2

dM ni , nj = | xi - xj | + | yi - yj |

dC ni , nj = max | xi - xj | , | yi - yj |

ここで，距離定義 dE, dM, dC は， それぞれユークリッド，マンハッタン，チェビシェフ距離の定義に対応します．

また， 対応するテキストラベルの大きさに応じて， 各ボロノイ領域の縦横比を変更し， 領域がテキストラベルの形状に合わせて水平方向に長くなるようにしました． さらに本手法では，等方的な各距離定義に異方性を組み込み， 各距離定義を次のように書き換えることにします．

dE ni , nj = xi - xj 2 + α yi - yj 2

dM ni , nj = | xi - xj | + α | yi - yj |

dC ni , nj = max | xi - xj | , α | yi - yj | ,

ここで， αはそれぞれのラベルの形に対応した， ボロノイ領域の縦横比であるとする． 図2に示すように， 限られたスクリーン空間内で， 重なりなく配置できるラベルの個数を調べることで， 3つの距離定義とその等方性および異方性のあるものを比較してみました． この結果， 異方性のあるチェビシェフ距離が， 対応するボロノイ分割が，一番勝つ多く不要な重なりなくラベルを配置できるという点で， 最適であることが示されました． したがって， 本提案手法では， ボロノイ分割を作成する際に， この距離定義を用いることとしました．

(a) 108 個の重なりを含むラベル (b) 81 個の重なりを含むラベル (c) 123 個の重なりを含むラベル
(d) 28 個の重なりを含むラベル (e) 78 個の重なりを含むラベル (f) 12 個の重なりを含むラベル
図2: 重心ボロノイ分割に基づくラベルの充填． 赤色のラベルは， 他のラベルと重複していることを示しています． 距離と異方性の選択は， 重なりをもつラベルの個数に大きな影響を与えます．


結果

図3は， 中規模ネットワークb124について， 従来の力学指向手法， 本提案手法， およびボロノイ領域を利用してラベルを配置する過去の手法よって作成された， 3つのレイアウトの視覚的比較を提供します． また， 図4に示すように， スモールワールドネットワークに適用することにより， 提案された手法を検証を行いました． これらの比較結果により， 提案手法は，力学指向アプローチによって得られたレイアウトと重心ボロノイ分割によって得られたレイアウトとの間の， 合理的な妥協点を確立できることが明らかになり， したがってそれぞれのノード周辺に十分なラベルを置く空間を確保できていることがわかります．

(a) (b) (c)
Fig. 3: b124ネットワークの可視化． (|V|=79, |E|=281). (a) 力学指向手法によるレイアウト(O = 5.9%)． (b) 提案手法によるレイアウト(T = 13.1 sec, O = 0.0%)． (c) ボロノイ分割を模倣した手法によるレイアウト(O = 0.0%)．各ボロノイ領域は異なる色で塗られている． ここで，|V|, |E|, T, O は， 頂点数，稜線数，計算時間，ラベル全体の面積に対する重なり部分の面積の比率を表しています．


(a) (b) (c)
Fig. 4: スモールワールド・ネットワークの可視化． (|V|=151, |E|=151). (a) 力学指向手法によるレイアウト(O = 2.7%)． (b) 提案手法によるレイアウト(T = 8.7 sec, O = 0.0%)． (c) ボロノイ分割を模倣した手法によるレイアウト(O = 0.0%)．各ボロノイ領域は異なる色で塗られている． ここで，|V|, |E|, T, Oは， 頂点数，稜線数，計算時間，ラベル全体の面積に対する重なり部分の面積の比率を表しています．


Papers

Hsiang-Yun Wu, Shigeo Takahashi, and Rie Ishida,   Overlap-Free Labeling of Clustered Networks Based on Voronoi Tessellation,   Journal of Visual Languages & Computing, Vol. 44, pp. 106-119, 2018.   [PDF], [DOI: 10.1016/j.jvlc.2017.09.008].

Rie Ishida, Shigeo Takahashi, and Hsiang-Yun Wu,   Adaptive Blending of Multiple Network Layouts for Overlap-Free Labeling,   In Proceedings of the 20th International Conference on Information Visualisation (IV2016), Lisbon, Portugal, (July, 2016), pp. 15-20, 2016.   [PDF], [DOI: 10.1109/IV.2016.25].

Rie Ishida, Shigeo Takahashi, and Hsiang-Yun Wu,   Interactively Uncluttering Node Overlaps for Network Visualization,   In Proceedings of the 19th International Conference on Information Visualisation (IV2015), Barcelona, Spain, (July, 2015), pp. 200-205, 2015.   [PDF], [DOI: 10.1109/iV.2015.44].

email