Abstract
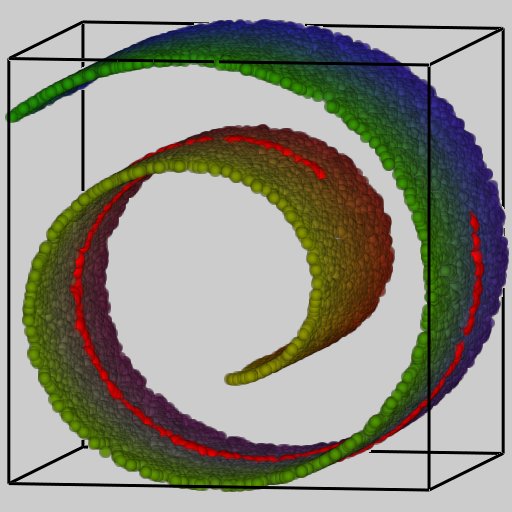
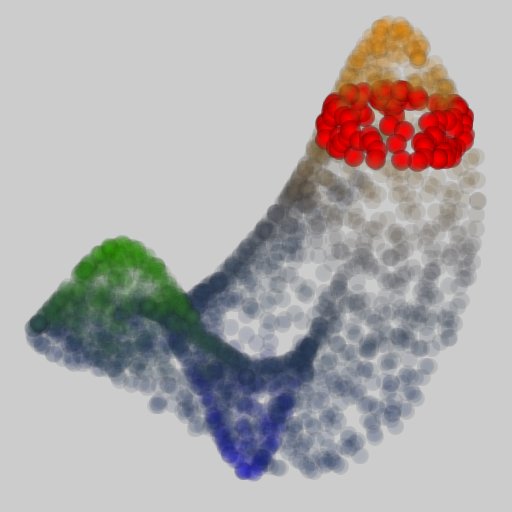
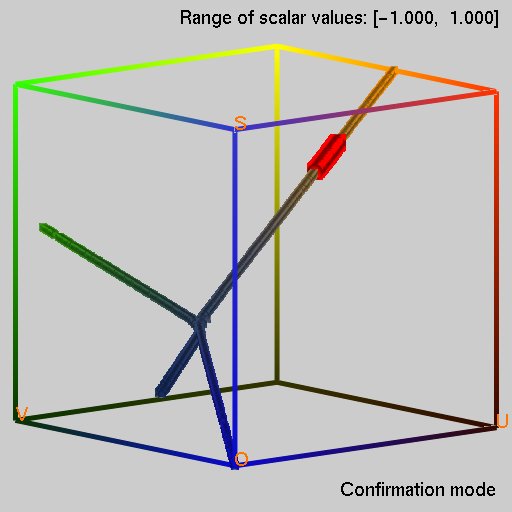
A contour tree is a powerful tool for delineating the topological evolution of isosurfaces of a single-valued function, and thus has been frequently used as a means of extracting features from volumes and their time-varying behaviors. Several sophisticated algorithms have been proposed for constructing contour trees while they often complicate the software implementation especially for higher-dimensional cases such as time-varying volumes. This paper presents a simple yet effective approach to plotting in 3D space, approximate contour trees from a set of scattered samples embedded in the high-dimensional space. Our main idea is to take advantage of manifold learning so that we can elongate the distribution of high-dimensional data samples to embed it into a low-dimensional space while respecting its local proximity of sample points. The contribution of this paper lies in the introduction of new distance metrics to manifold learning, which allows us to reformulate existing algorithms as a variant of currently available dimensionality reduction scheme. Efficient reduction of data sizes together with segmentation capability is also developed to equip our approach with a coarse-to-fine analysis even for large-scale datasets. Examples are provided to demonstrate that our proposed scheme can successfully traverse the features of volumes and their temporal behaviors through the constructed contour trees.
Paper & Video
|