Next: About this document ...
Up: No Title
Previous: Є°∆§їцєа
§≥§≥§«§ѕ°Ґ∞ћЅк≥—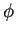 §ђ
§ђ
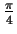 §ќЊмєз§тќг§»§Ј§∆Љ®§є°£
§ќЊмєз§тќг§»§Ј§∆Љ®§є°£
јµЄє«»
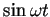 °Ґ
°Ґ
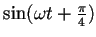 °Ґ§™§и§”
°Ґ§™§и§”
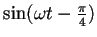 §ќ•∞•й•’§т≤Љњё§Ћ§ЋЉ®§є°£
§ќ•∞•й•’§т≤Љњё§Ћ§ЋЉ®§є°£
Figure 10:
њ §я∞ћЅк§ќјµЄє«»
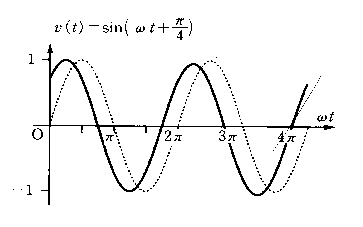 |
Figure 11:
√ў§м∞ћЅк§ќјµЄє«»
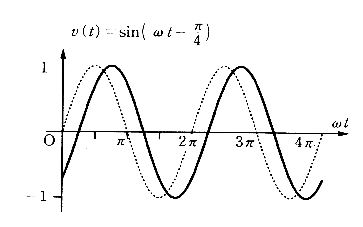 |
≈јјю§ќ
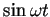 §тірља§Ћ§»§л§»Љ¬јю§ќ
§тірља§Ћ§»§л§»Љ¬јю§ќ
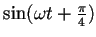 §ѕ∞ћЅк§ђ
§ѕ∞ћЅк§ђ
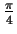 §ј§±њ §я°ҐЉ¬јю§ќ
§ј§±њ §я°ҐЉ¬јю§ќ
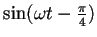 §ѕ∞ћЅк§ђ
§ѕ∞ћЅк§ђ
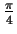 §ј§±√ў§м§∆§§§л°Ґ§»ƒкµЅ§µ§м§∆§§§л°£
§њ§ј§Ј°Ґ∞ћЅк§ќ°÷њ §я°Ґ√ў§м°„§ѕЅк¬–≈™§ §в§ќ§«§Ґ§к°Ґ
§ј§±√ў§м§∆§§§л°Ґ§»ƒкµЅ§µ§м§∆§§§л°£
§њ§ј§Ј°Ґ∞ћЅк§ќ°÷њ §я°Ґ√ў§м°„§ѕЅк¬–≈™§ §в§ќ§«§Ґ§к°Ґ
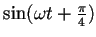 §тірља§Ћ§є§м§–°Ґ
§тірља§Ћ§є§м§–°Ґ
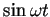 §ѕ
§ѕ
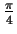 §ј§±√ў§м§∆§§§л§≥§»§Ћ§ §л°£
§ј§±√ў§м§∆§§§л§≥§»§Ћ§ §л°£
§Ј§њ§ђ§√§∆°Ґ њё§Ђ§й ђ§Ђ§л§и§¶§Ћ§Ґ§л«»ЈЅ§ђ°Ґірља§»§є§л«»ЈЅ§ќЇЄ¬¶§Ћ§Ґ§л§»§≠§ѕ∞ћЅк§ђњ §я°Ґ±¶¬¶§Ћ§Ґ§л§»§≠§Ћ§ѕ∞ћЅк§ђ√ў§м§∆§§§л§≥§»§Ћ§ §л°£
ƒЊќуґ¶њґ§ќЉ¬Є≥§Ћ§™§§§∆ љ–ќѕ≈≈∞µVR§»(ірља§»§Ј§њ)∆юќѕ≈≈∞µV§ќі÷§ќ∞ћЅк≥—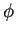 §ѕ
§ѕ
FG(•’•°•у•ѓ•Ј•з•у•Є•®•Ќ•м°Љ•њ)§«»ѓњґЉю«»њфf§т —§®§∆є‘§ѓ§»°Ґ
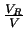 §ќ¬з§≠§µ§ђ —≤љ§є§л§»ґ¶§Ћ°ҐVR§»V§ќ«»ЈЅ§ќЅк¬–∞ћ√÷(∞ћЅкЇє)§ђЊеµ≠§ќ§и§¶§Ћ —≤љ§Ј§∆§§§ѓ§ќ§ті—ї°§«§≠§лО°
§ќ¬з§≠§µ§ђ —≤љ§є§л§»ґ¶§Ћ°ҐVR§»V§ќ«»ЈЅ§ќЅк¬–∞ћ√÷(∞ћЅкЇє)§ђЊеµ≠§ќ§и§¶§Ћ —≤љ§Ј§∆§§§ѓ§ќ§ті—ї°§«§≠§лО°
Kenichi Kuroda
2000-06-24