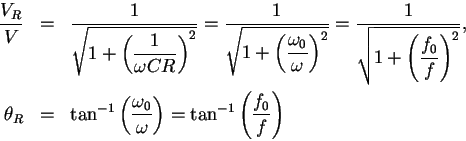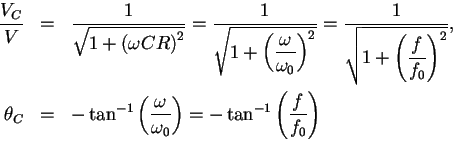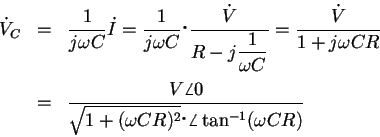
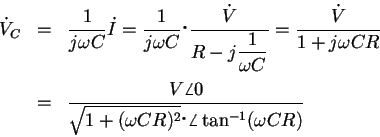
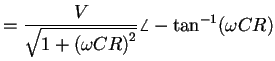 |
(2) |
 |
(3) |
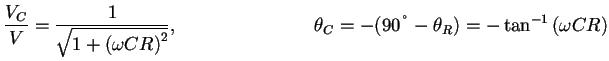 |
(4) |
そこで、与えられたRC(時定数)に対して周波数f(
![]() )を
変化させ、出力電圧/入力電圧、および位相角を測定すれば、
フィルタ特性(周波数特性)が得られる。
)を
変化させ、出力電圧/入力電圧、および位相角を測定すれば、
フィルタ特性(周波数特性)が得られる。
また、
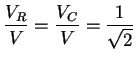 になる角周波数(または周波数)
になる角周波数(または周波数)
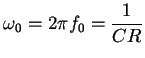 をカットオフ(cut-off)周波数と呼び、
この回路を通過させる周波数の目安を与えるので、回路を特徴づける量
として使われている。
また、このカットオフ周波数をグラフから読むには
定常的な電圧比から-3dB(
をカットオフ(cut-off)周波数と呼び、
この回路を通過させる周波数の目安を与えるので、回路を特徴づける量
として使われている。
また、このカットオフ周波数をグラフから読むには
定常的な電圧比から-3dB(
![]() )になった点の
周波数を読む。
入出力電圧の比を
)になった点の
周波数を読む。
入出力電圧の比を
![]() で表すと、
で表すと、