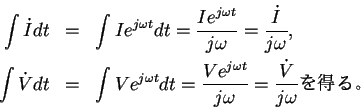Next: を使ったおおまかな微分、積分演算法(RC 回路)
Up: 微分、積分回路演算
Previous: 微分、積分回路演算
一定周波数の正弦波関数で表示される電流、電圧の指数関数表示は、
これらを 時間で微分すると、
となり、それぞれ、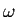 倍され、位相が
倍され、位相が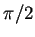 進むことを示してい
る。
これは、
進むことを示してい
る。
これは、
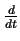 を一つの演算子として考えると、
を一つの演算子として考えると、
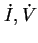 を時間で微分することは、
を時間で微分することは、
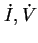 に
に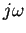 を掛け
てやることと同じである。
すなわち、次のようにおくことができる。
を掛け
てやることと同じである。
すなわち、次のようにおくことができる。
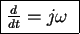
次に、
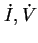 を時間で積分すると、
を時間で積分すると、
同じように、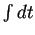 を一つの演算子と考えると、
を一つの演算子と考えると、
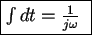
とおくことができる。
| すなわち、 |
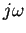 を掛けることは時間で微分すること、
を掛けることは時間で微分すること、 |
| |
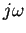 で割ることは時間で積分することである。
で割ることは時間で積分することである。 |
したがって、「微分方程式」を、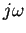 を含む「代数方程式」に変換
し、これを解き、簡単に解を求めることもできる(記号法)。
を含む「代数方程式」に変換
し、これを解き、簡単に解を求めることもできる(記号法)。
Kenichi Kuroda
2000-06-24
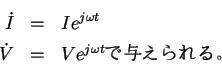
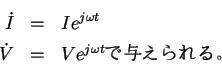
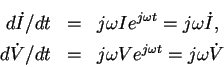
![]() を時間で積分すると、
を時間で積分すると、