物体の特徴をとらえる最適視点選択
研究内容
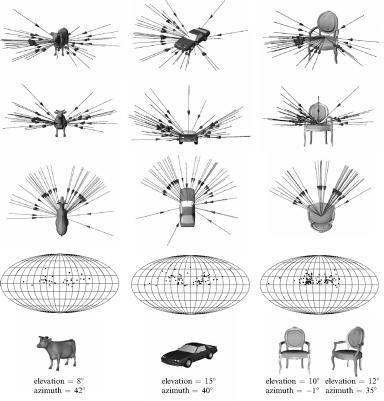
我々は3次元の情報を, 紙面やコンピュータディスプレイなど, 2次元の媒体を通して伝達するのが一般的です. その際, 3次元情報を2次元情報に変換する際の視点の選択は, 伝達できる3次元情報の量を大きく左右します. また,複数の視点からの投影図を作成することができても, 人は第一印象を少なからず左右されることが多く, 最初に一番最適な視点で3次元情報をとらえることが, 重要な課題と考えられます. 下図に示されている, V. Blanz (V. Blanz et al. Perception 28(5):575-600, 1999)らによる, 視点選択に関する心理学実験によると, 人が最適と思う視点は,
- 投影図の中に重要な特徴が多く含まれている.
- 視点を少し変更しても見えが劇的に変わらず安定してしている.
- 遮蔽されている部分が少ない.
|
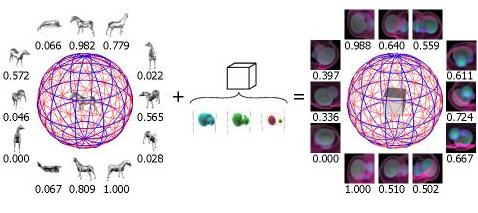
そこで本研究は, この知見をボリューム可視化に適用する手法を開発しました. 具体的には, 下図のようにまずボリュームの特徴解析を行います(中). その後, ボリュームデータを覆う球面上に視点サンプルをとり, それぞれの特徴に関してその視点の良さをスコアとして計算します(左). 最後に, それぞれの特徴に関するスコアの和をとり, 全体として妥協点となるような視点を最適なものとして選びます(右).
|
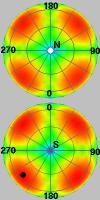
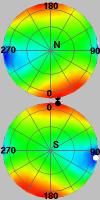
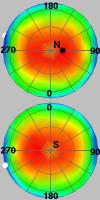
各特徴における最適視点の選択は, その特徴を構成する要素の見え具合いを確率としてとらえ, その情報エントリピーを最大化することで求めていきます. 例えば,正方形と馬の形状では, 最適視点(左)と最悪視点(右)は下図のようになります. ここで,対象を覆う球面上の視点評価値の分布(中)は, 赤い部分が高いスコア,青い部分が低いスコアを示し, 上が北半球から見たスコア分布, 下が南半球から見たスコア分布を表します. この分布で,白い点が最適視点の位置, 黒い点が最悪視点の位置を示します.
| 最適視点による投影図 | 視点評価値分布 | 最悪視点による投影図 |
|---|---|---|

|
|

|

|
|

|
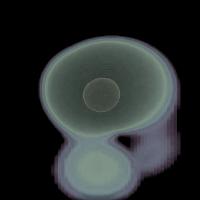
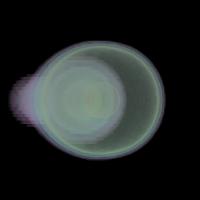
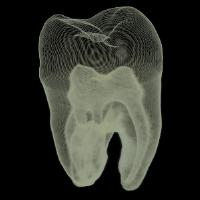
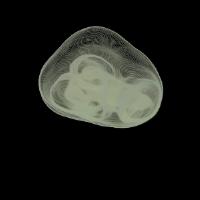
これをボリュームデータに適用した例を下図に示します. 下図の結果から分かる通り, 内部構造を含むボリュームデータに関しても, 視覚的に妥当な視点を最適なものとして計算できていることが分かります.
| 最適視点による投影図 | 視点評価値分布 | 最悪視点による投影図 |
|---|---|---|
|
|
|
|

|
|
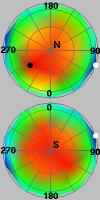
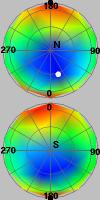
この手法の有効性を検証するため, ユーザテストを行いました. 具体的には, ユーザに様々な視点から見たボリュームデータの可視化結果を見てもらい, 対応する視点の良さを評価してもらい, そのスコアの分布と先に求めた分布を比較してみました. 下図がその結果ですが, 非常に振る舞いが似ている分布を得られることが分かり, 結果として, 提案手法が妥当な結果をもたらすことが示されます.

|
|

|
|
| 提案手法 | ユーザ評価 | 提案手法 | ユーザ評価 |
|
陽子 - 水素原子衝突 シミュレーションデータ |
歯のCTデータ | ||
参考資料
|
IEEE Visualization 2005 の発表ビデオ [WMV] |
参考文献
- S. Takahashi, I. Fujishiro, Y. Takeshima, and T. Nishita: "A Feature-Driven Approach to Locating Optimal Viewpoints for Volume Visualization," in Proc. of IEEE Visualization 2005, (at Minneapolis, MN, USA), IEEE Computer Society Press, pp. 495--502, October, 2005. [PDF]
- 高橋 成雄, 藤代 一成, 竹島 由里子, 西田 友是:
「ボリューム可視化のための最適視点位置計算」
Visual Computing/グラフィクスとCAD合同シンポジウム 2005,
pp. 35-40, June, 2005.
(情報処理学会グラフィクスとCAD研究会GCAD賞受賞)