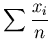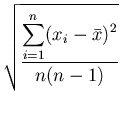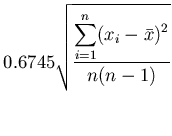Next: 最小二乗法
Up: 誤差と最小二乗法
Previous: 測定に関する用語の説明
ある物理量の真の値x0であるとする。この量を同じ条件で数多く測定
する時、統計誤差はなく、偶然誤差のみが誤差の原因であるとすると、測
定値xは真の値x0のまわりにランダムに分布しており、xがx0か
ら離れるほど、その値が測定される確率は小さくなる筈である。確率論に
よれば、xはガウス分布(正規分布ともいう)をしており、その分布関
数は、
| f(x) |
= |
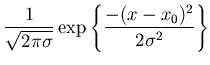 |
(1) |
Figure 2:
ガウス分布
![\begin{figure}
\begin{center}
\leavevmode
\psbox[scale=0.6]{me-ex1-fig2.eps} \end{center}\end{figure}](img22.gif) |
と表され、図 2に示すようにx=x0(真の値)でピークを示す。
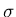 は標準偏差とよばれ、分布の広がりを表す量である。ある量を
n回測定して得られた測定値を
は標準偏差とよばれ、分布の広がりを表す量である。ある量を
n回測定して得られた測定値を
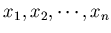 とすると、各測定
値に含まれる誤差はxi-x0であり、この誤差の二乗の平均を
とすると、各測定
値に含まれる誤差はxi-x0であり、この誤差の二乗の平均を
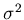 とすると、
とすると、
である。したがって、その平方根の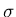 は、
は、
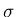 |
= |
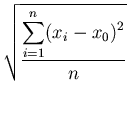 |
(2) |
と計算される。関数f(x)のすそ野は、
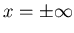 まで続いているが、
図 2のように
まで続いているが、
図 2のように
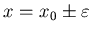 で狭まれる領域を考え、そ
の面積が全面積の1/2になる場合、すなわち全データの1/2がその中に含ま
れるように
で狭まれる領域を考え、そ
の面積が全面積の1/2になる場合、すなわち全データの1/2がその中に含ま
れるように
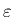 を選ぶと、
を選ぶと、
から、
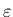 |
= |
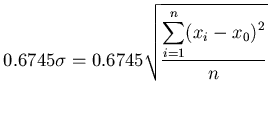 |
(3) |
となる。この値を確率誤差という。
しかしながら、我々はいくら実験を繰り返しても、真の値x0を知らな
いと
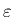 を計算することはできない。そこでn回の測定から推
測される最も確からしい値として平均値
を計算することはできない。そこでn回の測定から推
測される最も確からしい値として平均値
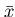 |
= |
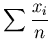 |
(4) |
を考えてみる。まず、n回の測定を行なって平均値
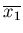 を
求め、またn回の測定を行なって平均値
を
求め、またn回の測定を行なって平均値
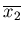 を求めると、
それらは必ずしも同じではない。すなわち、
を求めると、
それらは必ずしも同じではない。すなわち、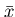 もx0の周
りに分布している筈である。しかし、nが大きくなれば
もx0の周
りに分布している筈である。しかし、nが大きくなれば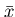 もx0に近い筈で、分布の広がりは
もx0に近い筈で、分布の広がりは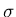 よりずっと狭いであろうと
考えられる。統計学によれば、この
よりずっと狭いであろうと
考えられる。統計学によれば、この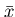 の標準偏差
の標準偏差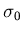 は、
は、
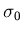 |
= |
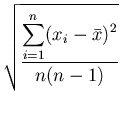 |
(5) |
となる。先に求めた
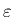 の表現で
の表現で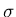 の代わりにこの
の代わりにこの
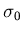 を用いると、
を用いると、
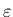 |
= |
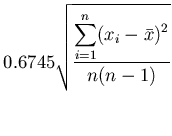 |
(6) |
となるが、これを平均値の確率誤差という。平均値はいくらでも詳しく計
算することができるが、それがどの桁まで信用できるか(有効数字)を知
るにはここに示した平均値の確率誤差を求めてみると良い。
Kenichi Kuroda
2000-06-23
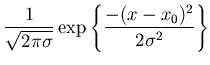
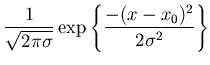
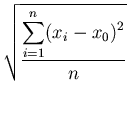
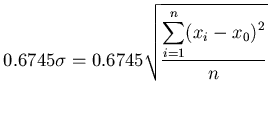
![]() を計算することはできない。そこでn回の測定から推
測される最も確からしい値として平均値
を計算することはできない。そこでn回の測定から推
測される最も確からしい値として平均値