最小二乗法

誤差が一方に起こるのと、反対方向に起こるのとが同じ程度に期待される 時は、算術平均値が最も確からしい値を与える。しかし、算術平均をとる 場合には、誤差が代数的に計算されるから、正負を打ち消してゼロになる ので、絶対値の大小が表面に現れなくなる。

そこで、誤差の二乗の和をとると、これはゼロにはならないから、「誤差 の二乗の和が最小」になるような平均値を求めて、それを最も確からしい 値とするのが最小二乗法(method of least squares)である。

＜注意＞

最小二乗法は最も確からしい平 均値を求める計算の一つの手段であって、測定した値の精度を高める方 法ではない。また、この方法を使うには、測定値がかなり正確であると ともに、個数が相当多くなければ効果は少ない。

★

一次実験式 y＝ax＋bの場合
一つの物理量xを変化させながら、他方の物理量yを何回か測定して、 両者の間の最も確からしい関係式、すなわち実験式を求めるのに、最小 二乗法が用いられている。これは、グラフによる平均化に対応する。

xの測定値を $x_1,x_2,\cdots,x_n$とし、それに対応するyの測定値 を $y_1,y_2,\cdots,y_n$とすると、次のn個の観測方程式が得られる。

$$\begin{eqnarray*}y_1 &=& ax_1+b\\ y_2 &=& ax_2+b \end{eqnarray*}$$

 

$$\vdots$$ (7)

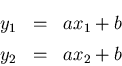
y_n &=& ax_n+b

いま、実験式を

 

y = ax+b (8)

とすると、xの測定値 $x_1,x_2,\cdots,x_n$を式(8)に代入して得 られる各yの値は、式(7)の $y_1,y_2,\cdots,y_n$の値と少しず つ異なる。しかし、もし式(8)が最も確からしい関係式であると すると、実測のy_iの値と、この式のxにx_iを入れて計算したyの 値ax_i+bとの差(残差)の二乗の和が最小になっているはずであるから (最小二乗法の原理)、

$$S = \sum (y_i-ax_i-b)^2 = 最小$$

が成り立つ。aおよびbについて最小でなければならないから、

$$\begin{eqnarray*}\frac{\partial S}{\partial a} &=& -2 \sum x_i(y_i-ax_i-b) = 0\\ \frac{\partial S}{\partial b} &=& -2 \sum (y_i-ax_i-b) = 0 \end{eqnarray*}$$

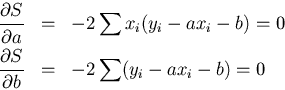
これを書き換えると

  

$$\left(\sum x_i^2\right)a + \left(\sum x_i\right)b \sum x_iy_i$$ = (9)

$$\left(\sum x_i\right)a + nb \sum y_i$$ = (10)

ここで、 $\sum x_i^2 = A, \sum x_i = B, \sum x_iy_i = C, \sum y_i = D$とおくと、これらの値は測定値x_i,y_iからそれぞれ求めることがで きる。式(9),(10)をa,bについて解くと、

$$\begin{eqnarray*}a &=& \frac{nC-BD}{nA-B^2} \end{eqnarray*}$$

 

$$\frac{AD-BC}{nA-B^2}$$ b = (11)

これが最も確からしい関係式(実験式)y=ax+bを求めることができる。

(例)ある銅線の電気抵抗Rを、温度tを変えながら測定したところ 表 1のような測定結果を得た。この銅線の0℃における抵抗 R₀と温度係数$\alpha$を求める。

 

 

Table 1: 電気抵抗Rの温度(t)依存性測定結果

ti[℃]	20	30	40	50	60
Ri[$\Omega$]	15.30	15.87	16.46	17.03	17.58

データより、温度t_iと抵抗R_iは、一次の関係式にあると考えられる。 このとき、温度tの抵抗Rは、

$$R=R_0(1+\alpha t) = R_0+R_0\alpha t$$

と表される。ここで、R₀は0℃における抵抗、$\alpha$は温度係数と 呼ばれる。式(8)と比較して、 $y \to R, \ x \to t,\ a \to R_0\alpha,\ b \to R_0$となるから、

$$\begin{eqnarray*}n &=& 5 \\ A &=& \sum t_i^2 = 9000 \\ B &=& \sum t_i = 200 \\ C &=& \sum t_iR_i = 3346.8 \\ D &=& \sum R_i = 82.24 \end{eqnarray*}$$

これらを式(11)に代入して、

$$\begin{eqnarray*}R_0\alpha &=& \frac{5 \times 3346.8 - 200 \times 82.24}{5\times... ...{9000\times 82.24-200\times3346.8}{5\times 9000-200^2} = 14.16 \end{eqnarray*}$$

したがって、

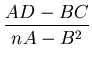
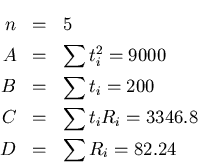
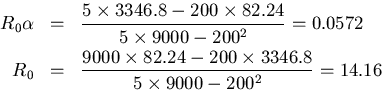
$$\begin{eqnarray*}\alpha &=& \frac{0.0572}{14.16} = 4.039\times 10^{-3} \\ R_0 &=& 14.16[\Omega ],\ \alpha = 4.039\times 10^{-3}[K^{-1}] \end{eqnarray*}$$

となる。