


Next: Q値
Up: LCR共振回路
Previous: LCR共振回路
直列共振回路のインピ−ダンス
インピ−ダンスの位相角(偏角)
ただし、
入力電圧を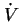 で表せば
で表せば
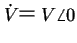 、すなわち位相0の
、すなわち位相0の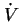 を基準とする。
を基準とする。
電流Iの大きさは、
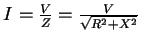
ここで、位相を入れてフェーザ表示すると
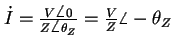
VRの大きさは、
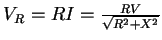
したがって、入出力比
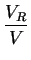 |
= |
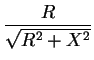 |
(7) |
位相を考慮し、フェーザ表示すると
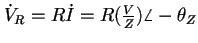 したがって、出力電圧
したがって、出力電圧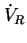 (位相は電流と同じ)と入力電圧
(位相は電流と同じ)と入力電圧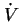 の間の位相差
の間の位相差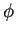 は
は
となる。すなわち、共振角周波数
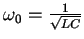 、または共振周波数
、または共振周波数
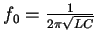 のとき両者の位相差
のとき両者の位相差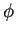 は0である。
は0である。
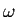 >
> 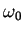 、すなわちf > f0のときは
、すなわちf > f0のときは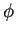 < 0で、電流の位相は入力電圧より
< 0で、電流の位相は入力電圧より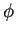 遅れる。
遅れる。
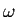 <
< 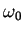 、すなわちf < f0のときは
、すなわちf < f0のときは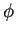 > 0で、電流の位相は入力電圧より
> 0で、電流の位相は入力電圧より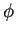 進むことになる。
進むことになる。
Kenichi Kuroda
2000-06-24
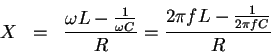
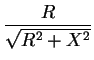
![$\displaystyle -\tan^{-1}(\frac{X}{R})=-\tan^{-1}[\frac{2\pi fL-\frac{1}{2\pi fC}}{R}]$](img78.gif)