Next: 実験
Up: LCR共振回路
Previous: 直列共振回路における出力電圧VRと入力電圧Vとの間の位相差
教科書76頁にあるように、f0における電流変化の鋭さを示す比帯域幅(または半値幅)は
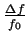 で表される。
で表される。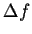 は共振電流の最大値(本実験では
は共振電流の最大値(本実験では
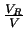 の値の最大値)の
の値の最大値)の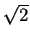 分の1のところでの共振曲線の幅(共振の幅という)である。
この共振の幅
分の1のところでの共振曲線の幅(共振の幅という)である。
この共振の幅
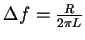 においての関係は計算で求めることができる。教科書では、コイルの質の良さを表す目安としてQ値という値を
においての関係は計算で求めることができる。教科書では、コイルの質の良さを表す目安としてQ値という値を
と定義している。
このQ値は 共振の鋭さ(または、コイルを含む共振回路の良さ)をも表し、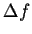 と次のような関係がある。
と次のような関係がある。
| Q |
= |
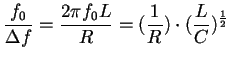 |
(9) |
これよりRの値が小さいとQ値が大きくなり、共振曲線が鋭くなる(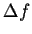 小)ことが分かる。この回路は、共振周波数f0の付近の周波数のみを通す性質をもっているので、共振(同調)フィルタ−と呼ぶこともある。
小)ことが分かる。この回路は、共振周波数f0の付近の周波数のみを通す性質をもっているので、共振(同調)フィルタ−と呼ぶこともある。
本実験では、この回路のf0、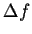 を実験的にグラフから求め、これよりQ値を求めよ。また、与えられたL、C、Rの値からf0、
を実験的にグラフから求め、これよりQ値を求めよ。また、与えられたL、C、Rの値からf0、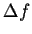 、Qを計算で求め、実験で求めた値と比較検討せよ。
、Qを計算で求め、実験で求めた値と比較検討せよ。
Kenichi Kuroda
2000-06-24