いままでは電源周波数が一定であったが、例えば、図
2.42(a)において、電圧![]() の周波数が変化した場合、合成インピーダンス
の周波数が変化した場合、合成インピーダンス
![]() もまた、次式により変化し、図(b)のような特性になる。
もまた、次式により変化し、図(b)のような特性になる。
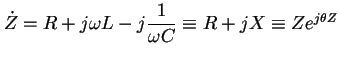 (2.74)
(2.74)
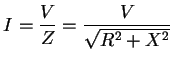 (2.75)
(2.75)
したがって、
![]() において、Zは最小値Rとなり、
電流は最大V/Rとなる。この状態を直列共振という。
において、Zは最小値Rとなり、
電流は最大V/Rとなる。この状態を直列共振という。
![]() は、X = 0とおいて、次式のように導かれる。
は、X = 0とおいて、次式のように導かれる。
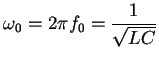 (2.76)
(2.76)
このf0を共振周波数という。また、図(c)の電流 - 周波数曲線を共
振曲線といい、
![]() における電流の鋭さを示す次式の比帯域幅
(または半値幅)が定義されている。
における電流の鋭さを示す次式の比帯域幅
(または半値幅)が定義されている。
普通、インダクタンスはコイルで構成されており、必ず抵抗がある。そこ で、抵抗Rが小さいほど電流曲線が鋭くなるので、これをコイルの質の 良さを表すQ値といい、次のように定義される。